Язык программирования R для анализа данных: лекция 12

Хи-квадрат, тест Фишера, Rmd/Quarto

Elena U

Тема лекции

Как выбрать статистический тест?
Тест хи-квадрат и тест Фишера для сравнения категориальных данных
~~Метод главных компонент~~
Поправки на множественное тестирование
Разбор Rmd/Quarto для создания красивых отчетов и презентаций в R

Как выбрать статистический тест?

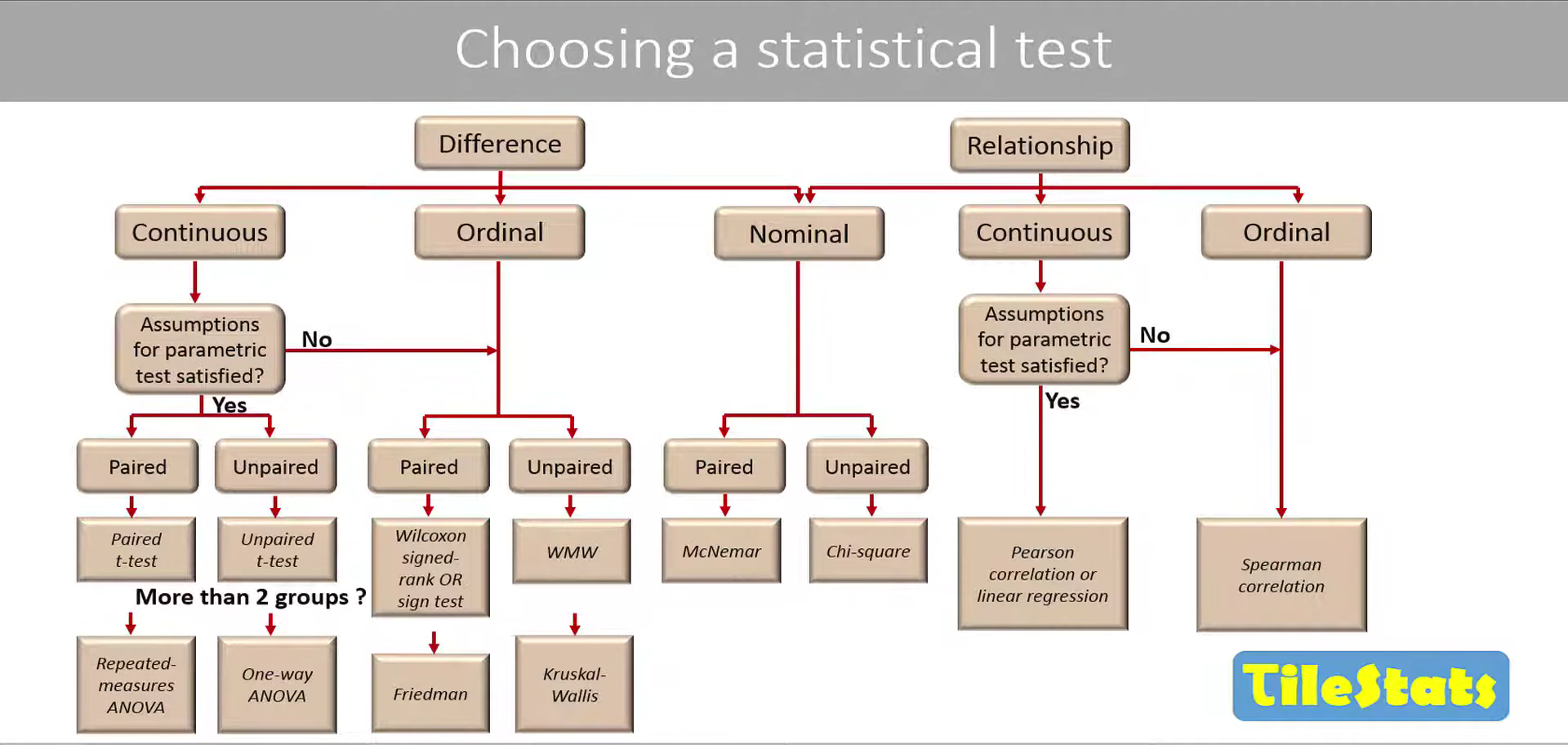
Взято с супер крутого канала по статистике TileStats

Работа с категориальными переменными

Таблицы сопряженности

Таблицы сопряженности (contingency tables) показывают, как частоты категорий по одной переменной зависят от значения другой категориальной переменной.

Можно узнать:

Различается ли вероятность быть съеденной птицей у светлых и темных улиток?
Насколько более вероятно развитие рака легких у курильщиков по сравнению с некурящими?
Будет ли ниже вероятность инфаркта у людей, принимающих аспирин?

Анализ сопряженности

Анализ сопряженности позволяет оценить, насколько связаны (“сопряжены”) друг с другом категориальные переменные.

Если переменные независимы, то значение одной из переменных не дает информации о вероятностях категорий другой переменной.

Слева — смерти среди 2092 пассажиров Титаника (данные из Dawson, 1995).

Справа — тот же график, если бы вероятность гибели не зависела от пола.

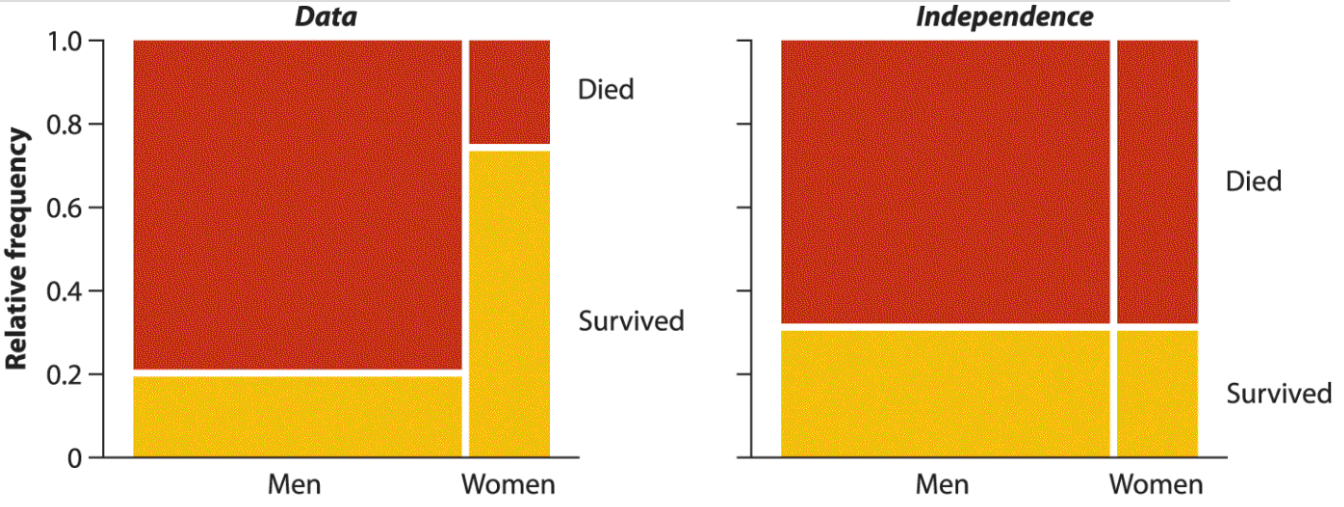
рис. 9.1-1 из Whitlock, Schluter, 2015

Тест $\chi^2$ для сравнения категориальных данных

Называется тест сопряженности хи-квадрат. Позволяет протестировать гипотезу о независимости категориальных переменных.

H₀ — категориальные переменные независимы друг от друга.

H₁ — категориальные переменные зависимы.

Возьмем старые данные по Warcraft 3, создадим переменную, обозначающую, является ли юнит призванным (is_summon):

library(tidyverse)
wc3_units <- read_tsv('https://raw.githubusercontent.com/ubogoeva/tidyverse_tutorial/master/data/wc3_heroes.txt',
                      col_names = TRUE, 
                      na = '-', 
                      name_repair = 'minimal') %>% 
  janitor::clean_names() %>% 
  mutate(is_summon = (pop == 0) | is.na(pop))

Тест $\chi^2$ для сравнения категориальных данных

Попробуем посчитать, связаны ли переменные race и is_summon (является ли юнит призванным).

Для подсчета количества элементов в каждой категории есть функция table()

wc3_units %>% 
  select(race, is_summon) %>% 
  table()

        is_summon
race     FALSE TRUE
  Human     13    4
  N.Elf     16    3
  Orc       13    4
  Undead    12    6

wc3_units %>% 
  select(race, is_summon) %>% 
  table() %>% 
  chisq.test()

Warning in chisq.test(.): аппроксимация на основе хи-квадрат может быть
неправильной


    Pearson's Chi-squared test

data:  .
X-squared = 1.5684, df = 3, p-value = 0.6666

chisq.test(wc3_units$race, wc3_units$is_summon)


    Pearson's Chi-squared test

data:  wc3_units$race and wc3_units$is_summon
X-squared = 1.5684, df = 3, p-value = 0.6666

Визуализация данных хи-квадрат

wc3_units %>% 
  select(race, is_summon) %>% 
  table() %>% 
  mosaicplot()

Тест хи-квадрат может работать не совсем корректно, если в ячейках таблицы мало значений по какой-либо категории. В таком случае лучше воспользоваться точным тестом Фишера.

Точный тест Фишера: формула

Данные по мотивам статьи Reed and Janzen, 1999

Таблица 2x2:

	улитки съеденные	улитки живые	Всего
светлые	a=36	b=4	a+b
темные	c=50	d=446	c+d
	a+c	b+d	n

Формула:

\[ p = \frac{(a+b)!(c+d)!(a+c)!(b+d)!}{n!a!b!c!d!} \]

Точный тест Фишера: запуск в R

Функция fisher.test() в базовом R.

snail_data <- data.frame(eaten = c(36, 50), not_eaten = c(4, 446), 
                         row.names = c('light', 'dark'))
snail_data

	eaten	not_eaten
light	36	4
dark	50	446

fisher.test(snail_data)


    Fisher's Exact Test for Count Data

data:  snail_data
p-value < 2.2e-16
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
  26.76618 317.39716
sample estimates:
odds ratio 
  78.82281

Многомерный анализ данных

Метод главных компонент (Principal Component Analysis, PCA)
Многомерное шкалирование (Multidimensional Scaling, MDS)
Кластерный анализ
Факторный анализ
Дискриминантный анализ

Поправки на множественное тестирование

Существует 2 принципиально разных подхода к поправкам на множественное тестирование.

Контроль групповой вероятности ошибки I рода (FWER, family-wise error rate)
- Тесты для попарных сравнений групп: пост-хоки (поправка Тьюки, поправка Даннета, тест Фишера LSD и тд)
- Тесты, которые поправляют значимость у набора p-value (поправка Бонферрони, Холма-Бонферрони и тд)
Контроль доли ложных открытий (FDR, false discovery rate): поправка Benjamini-Hochberg, поправка Benjamini-Yekutieli.

Начнем разбор с первого способа

FWER – family-wise error rate

FWER – вероятность совершить хоть одну ошибку первого рода.

\[ FWER = 1 - (1-\alpha)^k, \]k - количество тестов, $\alpha$ - уровень значимости.

Для корректного применения формулы тесты должны быть независимыми.

Если это не так, то посчитать точный FWER можно с помощью симуляции, а по формуле вычисляется верхняя граница (то есть максимально возможное значение вероятности совершить ошибку I рода).

Пример ситуаций, когда тесты зависимы:

Собрали две группы образцов и измерили у них 20 параметров. Тесты зависимы, поскольку пул образцов один и тот же для каждого измеренного параметра.
У нас 3 группы, делаем попарное сравнение каждой группы с каждой. Тесты зависимы, поскольку одна и та же группа участвует в двух тестах.

Симуляция независимых тестов для подсчета FWER

Генерируем выборки размером 100 из одной генеральной совокупности (стандартного нормального распределения) и сравниваем их t-тестом 10000 раз. Считаем, в скольких процентах случаев из заданного количества тестов (5, 10, 50, 100) мы получили p-value < 0.05.

Тесты независимые, поскольку каждый раз извлекаем новую выборку.

mean(replicate(10000, sum(replicate(5, t.test(rnorm(100), rnorm(100))$p.value) < 0.05) != 0))

[1] 0.2179

mean(replicate(10000, sum(replicate(10, t.test(rnorm(100), rnorm(100))$p.value) < 0.05) != 0))

[1] 0.3975

mean(replicate(10000, sum(replicate(50, t.test(rnorm(100), rnorm(100))$p.value) < 0.05) != 0))

[1] 0.9195

mean(replicate(10000, sum(replicate(100, t.test(rnorm(100), rnorm(100))$p.value) < 0.05) != 0))

[1] 0.9934

Поправка Бонферрони (Bonferroni)

Самый простой способ контролировать вероятность ошибки первого рода – это изменить критический уровень значимости.

\[ FWER = 1 - (1-\frac{\alpha}{k})^k, \]

Делим $\alpha$ на число тестов -> получаем новый p-уровень значимости, ниже которого результаты будут считаться статистически значимыми.

Или умножаем каждое p-value на количество тестов -> если поправленное p-value < 0.05, то результат считается статистически значимым.

При таком подходе мы контролируем вероятность ошибки первого рода, однако завышаем вероятность ошибки второго рода -> уменьшаем мощность теста.

Поправка Бонферрони (Bonferroni)

Проверим FWER после поправки.

mean(replicate(10000, sum(replicate(5, t.test(rnorm(100), rnorm(100))$p.value) < 0.05/5) != 0))

[1] 0.0547

mean(replicate(10000, sum(replicate(10, t.test(rnorm(100), rnorm(100))$p.value) < 0.05/10) != 0))

[1] 0.0459

mean(replicate(10000, sum(replicate(50, t.test(rnorm(100), rnorm(100))$p.value) < 0.05/50) != 0))

[1] 0.0474

mean(replicate(10000, sum(replicate(100, t.test(rnorm(100), rnorm(100))$p.value) < 0.05/100) != 0))

[1] 0.0504

Контролирует вероятность совершить хоть 1 ошибку I рода на заданном уровне 0,05. В итоге страдает мощность теста.

Поправка Холма

Более мягкая поправка. Разберем на примере как работает.

p_value <- c(0.004, 0.87, 0.003, 0.04, 0.18, 0.24)

Сортируем и ранжируем p-value по убыванию, далее по формуле умножаем каждое p-value на $(m+1-rank)$, где $m$ - количество тестов, $rank$ - ранг p-value.

pvalue	rank_pvalue	formula	result
0.003	1	0.003*(6 + 1 - 1)	0.018
0.004	2	0.004*(6 + 1 - 2)	0.020
0.040	3	0.04*(6 + 1 - 3)	0.160
0.180	4	0.18*(6 + 1 - 4)	0.540
0.240	5	0.24*(6 + 1 - 5)	0.480
0.870	6	0.87*(6 + 1 - 6)	0.870

Далее нужно задать, что поправленные p-value могут только возрастать.

Поправка Холма

pvalue	rank_pvalue	formula	result	p_adjusted
0.003	1	0.003*(6 + 1 - 1)	0.018	0.018
0.004	2	0.004*(6 + 1 - 2)	0.020	0.020
0.040	3	0.04*(6 + 1 - 3)	0.160	0.160
0.180	4	0.18*(6 + 1 - 4)	0.540	0.540
0.240	5	0.24*(6 + 1 - 5)	0.480	0.540
0.870	6	0.87*(6 + 1 - 6)	0.870	0.870

На самом деле я здесь схитрила и последнюю колонку посчитала функцией p.adjust()

Можем убедиться, что у нас подсчитано все верно:

p.adjust(sort(p_value), method = 'holm')

[1] 0.018 0.020 0.160 0.540 0.540 0.870

Поправка Холма

Поскольку для самого минимального p-value поправленное p-value такое же как и у Бонферрони, то поправка Холма контролирует FWER на том же уровне 0.05 (что и поправка Бонферрони), при этом не так сильно снижает мощность тестов.

Проверим на 100 тестах:

replicate(1000, sum(replicate(100, t.test(rnorm(100), rnorm(100))$p.value) %>% p.adjust(method = 'holm') < 0.05) != 0) %>% mean()

[1] 0.049

Поправка Тьюки (Tukey)

\[ q_s = \frac{M_1 - M_2}{\sqrt{\frac{SS_w}{2}(\frac{1}{n_A}+\frac{1}{n_B})}}, \]

где M₁ > M₂ (средние в группе), nA, nB - размер 1 и 2 выборки, SS_W - внутригрупповая сумма квадратов в ANOVA.

Для проверки гипотезы используется studentized range distribution, студентизированное распределение.

Тестируется сравнение средних каждой группы с каждой, необязательно использовать только после значимой ановы (однако в тесте используется SS_W и количество степеней свободы из таблицы ановы).

Studentized range distribution

k - количество групп, df - количество степеней свободы в SS_W — количество наблюдений-количество групп.

Тест Даннета (Dunnet)

Тестирует сравнение контроля с остальными группами, используется в ситуации, когда не нужно сравнение каждой группы с каждой.

Как выбрать, какую поправку использовать?

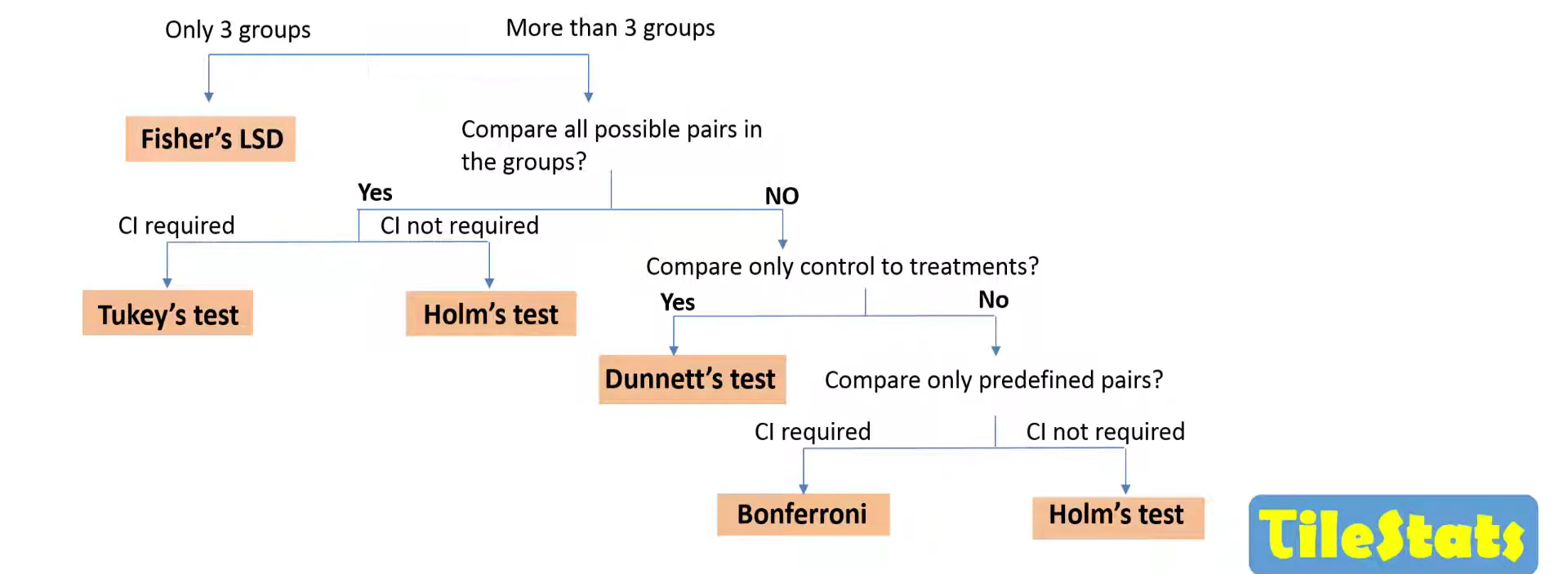
Картинка отсюда

FDR - false discovery rate

	H₀ верна (различий нет)	H₀ неверна (различие есть)
Не отклонить H₀	True Negative (TN)	False Negative (FN)
Отклонить H₀	False Positive (FP)	True Positive (TP)

\[ FDR = \frac{FP}{FP + TP} \]

Подробнее в этом видео

Расчет FDR

p_values <- c(0.361, 0.387, 0.005, 0.009, 0.022, 0.051, 0.101, 0.019)

Сортируем и ранжируем p-value по возрастанию
Каждое p-value умножаем на $\frac{m}{rank}$, где $m$ – количество тестов, $rank$ – ранг p-value

pvalue	rank_pvalue	formula	result
0.005	1	0.005*(8/1)	0.0400000
0.009	2	0.009*(8/2)	0.0360000
0.019	3	0.019*(8/3)	0.0506667
0.022	4	0.022*(8/4)	0.0440000
0.051	5	0.051*(8/5)	0.0816000
0.101	6	0.101*(8/6)	0.1346667
0.361	7	0.361*(8/7)	0.4125714
0.387	8	0.387*(8/8)	0.3870000

Расчет FDR

Итоговое FDR вычисляется так, чтобы p-value не убывали, но при этом приводится в меньшую сторону (в отличие от поправки Холма).

pvalue	rank_pvalue	formula	result	p_adjusted	reject_H0
0.005	1	0.005*(8/1)	0.0400000	0.0360000	yes
0.009	2	0.009*(8/2)	0.0360000	0.0360000	yes
0.019	3	0.019*(8/3)	0.0506667	0.0440000	yes
0.022	4	0.022*(8/4)	0.0440000	0.0440000	yes
0.051	5	0.051*(8/5)	0.0816000	0.0816000	no
0.101	6	0.101*(8/6)	0.1346667	0.1346667	no
0.361	7	0.361*(8/7)	0.4125714	0.3870000	no
0.387	8	0.387*(8/8)	0.3870000	0.3870000	no

Работа с RMarkdown

Введение в RMarkdown и Quarto

File -> New File -> Markdown File

Markdown	Вывод
курсив и полужирный	курсив и полужирный
надстрочный^2^ / подстрочный~2~	надстрочный² / подстрочный₂
~~зачеркнутый~~	~~зачеркнутый~~
`vebratim code`	`vebratim code`

Заголовки

Markdown	Вывод
# Заголовок 1	Заголовок 1
## Заголовок 2	Заголовок 2
### Заголовок 3	Заголовок 3
#### Заголовок 4	Заголовок 4

Картинки и гиперссылки

[ссылка](https://github.com/ubogoeva/Rcourse_NSU)

ссылка

![](https://quarto.org/quarto.png)

Tip

В Quarto можно использовать визуальный редактор, который упрощает работу с Markdown-синтаксисом.

Формулы на основе LaTeX-синтаксиса

Математические формулы в Quarto используют разделители $ для встроенных математических элементов текста и разделители $$ для выносной математики на основе LaTeX-синтаксиса.

Markdown	Вывод
inline math: $E = mc^{2}$	inline math: \(E = mc^{2}\)
display math: $$E = mc^{2}$$	display math: \[E = mc^{2}\]

inline math: $E = mc^{2}$

display math:

$$E = mc^{2}$$

display math:

\[E = mc^{2}\]

Формулы на основе LaTeX-синтаксиса

Более сложный пример:

var = \frac{\sum_{i=1}^n{(x_i - \overline{x})^2}}{n-1}

\[ var = \frac{\sum_{i=1}^n{(x_i - \overline{x})^2}}{n-1} \]

Все формулы в рамках этого курса были сверстаны с использованием LaTeX, очень удобная штука, рекомендую.

Ячейки исполняемого кода

```{r}
head(iris)
```

  Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1          5.1         3.5          1.4         0.2  setosa
2          4.9         3.0          1.4         0.2  setosa
3          4.7         3.2          1.3         0.2  setosa
4          4.6         3.1          1.5         0.2  setosa
5          5.0         3.6          1.4         0.2  setosa
6          5.4         3.9          1.7         0.4  setosa

head(iris)

  Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1          5.1         3.5          1.4         0.2  setosa
2          4.9         3.0          1.4         0.2  setosa
3          4.7         3.2          1.3         0.2  setosa
4          4.6         3.1          1.5         0.2  setosa
5          5.0         3.6          1.4         0.2  setosa
6          5.4         3.9          1.7         0.4  setosa

Создадим Rmd документ

File -> New File -> R Markdown

Проиллюстрировать в R

Работа с Quarto

Сайт на Quarto, посвященный работе с Quarto с материалами на Quarto от Евгения Матерова.

У меня сайт курса и презентации тоже сделаны в Quarto.

Проиллюстрировать создание документа и презентации -> в новом проекте RStudio

Материалы для дальнейшего изучения

Книги и ютуб каналы:

Чаты по статистике и R

Набор курсов по R Марины Варфоломеевой (СПбГУ)

Спасибо всем за посещение курса!

Если понравилось, переходите по ссылке:

Язык программирования R для анализа данных: лекция 12

Тема лекции

Как выбрать статистический тест?

Работа с категориальными переменными

Таблицы сопряженности

Анализ сопряженности

Тест \(\chi^2\) для сравнения категориальных данных

Тест \(\chi^2\) для сравнения категориальных данных

Визуализация данных хи-квадрат

Точный тест Фишера: формула

Точный тест Фишера: запуск в R

Многомерный анализ данных

Поправки на множественное тестирование

FWER – family-wise error rate

Симуляция независимых тестов для подсчета FWER

Поправка Бонферрони (Bonferroni)

Поправка Бонферрони (Bonferroni)

Поправка Холма

Поправка Холма

Поправка Холма

Поправка Тьюки (Tukey)

Studentized range distribution

Тест Даннета (Dunnet)

Как выбрать, какую поправку использовать?

FDR - false discovery rate

Расчет FDR

Расчет FDR

Работа с RMarkdown

Введение в RMarkdown и Quarto

Заголовки

Заголовок 1

Заголовок 2

Заголовок 3

Заголовок 4

Картинки и гиперссылки

Формулы на основе LaTeX-синтаксиса

Формулы на основе LaTeX-синтаксиса

Ячейки исполняемого кода

Создадим Rmd документ

Работа с Quarto

Материалы для дальнейшего изучения

Спасибо всем за посещение курса!