Язык программирования R для анализа данных: лекция 6

Введение в статистику вывода

Elena U

Рекомендуемая литература

  • Книги:

    • “Статистика для всех” Сара Бослаф (Statistics in a Nutshell)

  • Курсы

Note

Больше источников здесь

План лекции

  • Типы переменных и типы шкал

  • Понятие генеральной совокупности и выборки

  • Описательные статистики

  • Статистика вывода

  • Тест Стьюдента, ограничения, особенности

Данные для работы

library(tidyverse)
wc3_units <- read_tsv('https://raw.githubusercontent.com/ubogoeva/tidyverse_tutorial/master/data/wc3_heroes.txt',
                      col_names = TRUE, 
                      na = '-', 
                      name_repair = 'minimal') %>% 
  janitor::clean_names() # для правильных названий колонок

Типы переменных и типы шкал

  • Количественные

    • Непрерывные (рост, вес, длина корня)

    • Дискретные (количество детей в семье)

    • Интервальные (температура в градусах Цельсия)

    • Ранговые (места в соревнованиях, тяжесть болезни)

  • Качественные (категориальные, номинативные)

    • Бинарные (есть мутация или нет)

Классификации типов переменных

Зависимые и независимые переменные - важно для проведения статистических критериев.

Что такое генеральная совокупность?

  • Генеральная совокупность — совокупность всех объектов (единиц), относительно которых предполагается делать выводы при изучении конкретной задачи.

  • Генеральная совокупность состоит из всех объектов, которые имеют качества, свойства, интересующие исследователя.

    Например: все клетки определенной клеточной линии, все растения определенного генотипа.

Что такое выборка?

  • Выборка — часть генеральной совокупности элементов, доступная для исследования.

Классификация выборки

  • По принципу отбора:

    • Независимые

    • Зависимые (например до и после применения лекарства)

  • По корректности отбора:

    • Репрезентативные

    • Нерепрезентативные

  • Основные стратегии отбора:

    • Простая случайная выборка

    • Стратифицированная

Как можно описать значения в выборке?

Описательные статистики:

  • Меры центральной тенденции

  • Меры изменчивости

Меры центральной тенденции

  • Среднее - среднее арифметическое всех значений.

  • Медиана - середина упорядоченного ряда значений.

  • Мода - наиболее часто встречающееся значение в выборке.

mean(wc3_units$gold) # среднее
[1] NA
mean(wc3_units$gold, na.rm = TRUE) # среднее без учета пропущенных значений
[1] 195.625
median(wc3_units$gold, na.rm = TRUE) # медиана
[1] 190

Для вычисления моды можно использовать функцию dplyr::count()

Вычисление моды: dplyr::count()

wc3_units %>% 
  count(armor_type)
# A tibble: 6 × 2
  armor_type       n
  <chr>        <int>
1 Fort             1
2 Heavy           29
3 Invulnerable     1
4 Light           11
5 Medium          15
6 Unarmored       14
wc3_units %>% 
  count(armor_type) %>% 
  arrange(desc(n))
# A tibble: 6 × 2
  armor_type       n
  <chr>        <int>
1 Heavy           29
2 Medium          15
3 Unarmored       14
4 Light           11
5 Fort             1
6 Invulnerable     1

Меры изменчивости

  • Размах – разность между максимальным и минимальным значениями.

  • Межквартильный размах – разница между верхним и нижним квартилем.

  • Дисперсия – сумма квадратов отклонений, деленная на их количество.

    Note

    Отклонение – это разность между средним арифметическим и конкретным значением.

  • Стандартное отклонение – корень из дисперсии.

Формула дисперсии и стандартного отклонения

Дисперсия (variance):

\[ var = \frac{\sum_{i=1}^n(x_i - \overline{x})^2}{n}, \]

где \(\overline{x}\) - среднее, n - количество элементов в выборке

Стандартное отклонение (standard deviation, sd)

\[ sd = \sqrt{var} =\sqrt{\frac{\sum_{i=1}^n(x_i - \overline{x})^2}{n}} \]

Здесь приведена смещенная оценка - то есть в знаменателе n.

По умолчанию функции var() и sd() считают несмещенную оценку - в знаменателе n-1.

Межквартильный размах или как интерпретировать боксплот

Боксплот

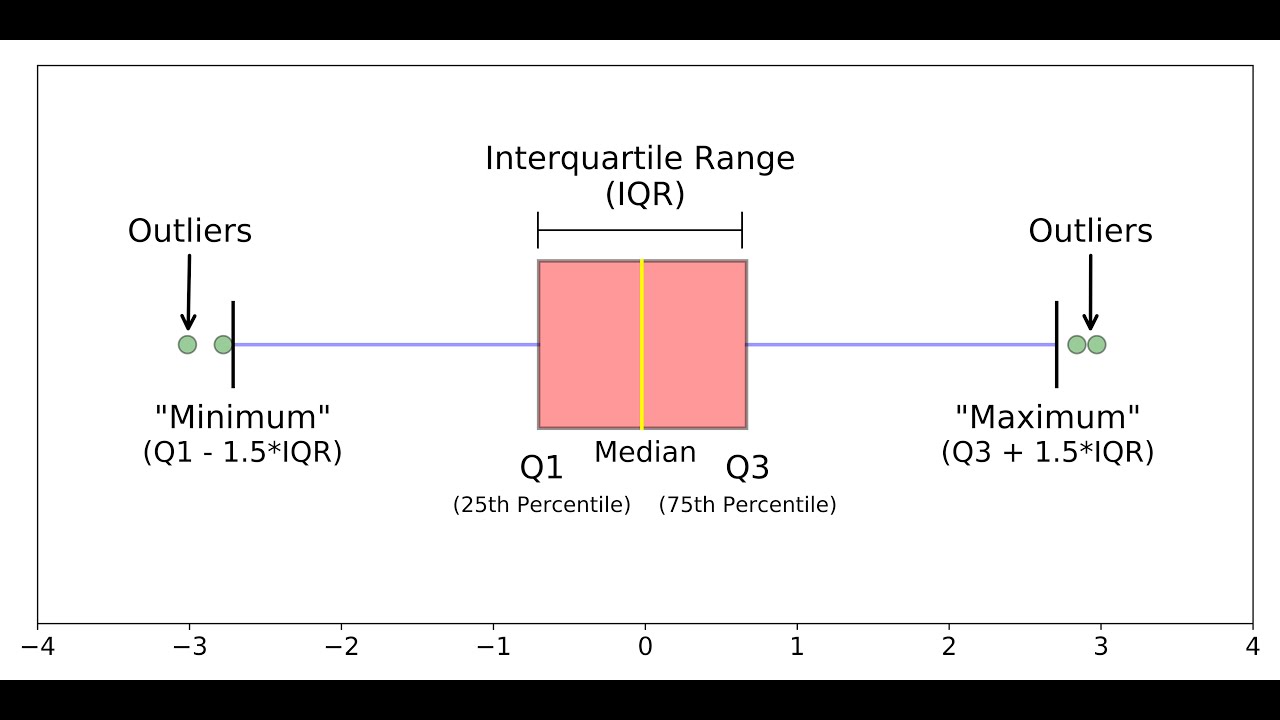
Оценки среднего

Стандартная ошибка

Доверительный интервал

Нормальное распределение

Непрерывное распределение вероятностей с пиком в центре и симметричными боковыми сторонами, которое в одномерном случае задаётся функцией плотности вероятности, совпадающей с функцией Гаусса.

set.seed(1)
norm_distr <- rnorm(10000)
hist(norm_distr, freq = FALSE)
lines(density(norm_distr))

Нормальное распределение

Центральная предельная теорема

Согласно центральной предельной теореме (ЦПТ, central limit theorem), какой бы ни была форма распределения в генеральной совокупности, выборочное распределение средних будет стремиться к нормальному. При этом чем больше размер выборки, тем ближе выборочное распределение средних будет к нормальному.

Центральная предельная теорема

Используем лог-нормальное распределение:

hist(rlnorm(10000), breaks = 100)

Как будут распределены средние из лог-нормального распределения?

many_means <- replicate(1000, mean(rlnorm(10000)))
hist(many_means, breaks = 100)

Они будут распределены нормально!

Тест Стьюдента

wc3_units_armor <- wc3_units %>% 
  filter(armor_type == 'Heavy' | armor_type == 'Light')
t.test(wc3_units_armor$hp ~ wc3_units_armor$armor_type)

    Welch Two Sample t-test

data:  wc3_units_armor$hp by wc3_units_armor$armor_type
t = -2.3602, df = 21.493, p-value = 0.02778
alternative hypothesis: true difference in means between group Heavy and group Light is not equal to 0
95 percent confidence interval:
 -536.65167  -34.28877
sample estimates:
mean in group Heavy mean in group Light 
           533.6207            819.0909